Neuronale Netzwerke – Was steckt dahinter?
Neuronale Netzwerke, Deep-Learning, Convolutional Neural Networks, Künstliche Intelligenz – all diese Begriffe tauchen in den letzten Jahren immer häufiger auf. Doch was genau verbirgt sich dahinter und wie funktionieren diese Konstrukte? Und vor allem: Welche Probleme können sie lösen?
Bilderkennung
Betrachten wir das Problem der Bilderkennung, im Speziellen die Zuordnung von Bildern handgeschriebener Ziffern zu den Zahlen 0-9. Schon diese sehr eingeschränkte Form der Bilderkennung wirft eine Menge Probleme auf, wenn man versucht einen Algorithmus zu finden, der sich mit den üblichen Programmiersprachen umsetzen lässt. Zur Veranschaulichung hier zwei Ansätze mit Erklärung:
- Ein Ansatz wäre das Reduzieren des Problems auf das Erkennen von einmaligen Formen einer jeden Ziffer, beispielweise zwei verbundene Kreise für eine Acht oder zwei in einem bestimmten Winkel aufeinander treffende Striche für eine Eins (oder Sieben?). Daraus ergibt sich aber ein weiteres Problem: Wie definiert und erkennt man etwas wie Kreise oder Striche? Letztendlich arbeitet man auf einer Liste von Zahlen, die die Farbwerte der Pixel des Bildes repräsentieren. Wie leitet man darauf geometrische Formen ab? Wie definiert man, welche Kombination von Formen welche Ziffer ergibt?
- Eine andere Möglichkeit wäre, das Eingabebild mit einem Referenzbild abzugleichen und einen Wert zu errechnen, der die Ähnlichkeit beider Bilder anzeigt – je höher dieser Wert, desto ähnlicher die Bilder. Durch Ausprobieren müsste man dann Schwellenwerte finden, unter denen ein Eingabebild als ähnlich genug zu einem Referenzbild betrachtet wird. Falls das Eingabebild auf mehrere Referenzbilder passt, wählt man dasjenige mit dem höchsten Ähnlichkeitswert. Aber auch bei diesem Ansatz gibt es Probleme: Woher nimmt man die Referenzbilder? Wie stellt man sicher, dass die Referenzbilder so ähnlich wie möglich zu korrekten Zahlen sind. Und wie genau berechnet man die Ähnlichkeit?
Bei beiden Möglichkeiten ergeben sich aus dem Ursprungsproblem weitere Probleme mit annähernd gleicher Komplexität. Das Problem mit traditionellen Methoden zu lösen, scheint unmöglich oder zumindest extrem aufwendig.
Die Lösung dieses Problems findet sich (wie so oft) in der Natur: Für ein menschliches (oder auch tierisches) Gehirn ist dieses Problem trivial. Bereits Kleinkinder können auf Bildern beliebige Objekte identifizieren und auch viele Tiere sind dazu fähig. Und an das Identifizieren von beliebigen Bildern durch einen traditionellen Algorithmus brauchen wir gar nicht erst zu denken, wie das obige Beispiel gezeigt hat.
Ein Gehirn funktioniert also grundlegend anders als traditionelle Computer. Es arbeitet nicht nach starren Algorithmen, sondern erkennt Muster in dem Gesehenen und kann aus diesen Mustern mit Hilfe früherer Erfahrungen Schlussfolgerungen ableiten. Voraussetzung dafür ist aber, ein ähnliches Muster schon einmal gesehen zu haben – wenn jemand noch nie etwas von Katzen gehört hat, kann man ein Katzenbild auch nicht korrekt klassifizieren. Der Lernprozess ist also von enormer Bedeutung. Aus diesem natürlichen Vorbild lässt sich eine Datenstruktur ableiten, mit der auch ein Computer solche Probleme bis zu einem gewissen Grad lösen kann: Ein neuronales Netzwerk.
Neuronale Netzwerke
Neuronale Netzwerke nehmen sich die Gehirne von intelligenten Lebewesen zum Vorbild, um Probleme zu lösen, die in der klassischen Informatik nur sehr schwer zu lösen sind. Wie der Name sagt, besteht ein neuronales Netzwerk (NN) aus Neuronen, die miteinander in einer bestimmten Weise vernetzt sind. Um zu verstehen, wie ein NN funktioniert, müssen wir beim Kleinsten beginnen: Einem Neuron.
Zur Modellierung eines Neurons gibt es das Konzept des Perceptrons:

Ein Perceptron hat eine beliebige Anzahl von Eingabewerten (hier x1 bis x3) und genau einen Ausgabewert. Ein- und Ausgabe sind binär, es ist also nur Null oder Eins zulässig. Jeder Eingabewert hat dabei eine Gewichtung (Weight, hier w1 bis w3), die jeweils eine beliebige Zahl sein kann. Zusätzlich hat das Perceptron einen Schwellenwert (Bias), ab dem es feuert (d.h. Eins als Ausgabe produziert). Das Perceptron liefert nur dann Eins als Ergebnis, wenn die Summe der Produkte aus Eingabewert und Gewichtung größer als der Schwellenwert ist. Mathematisch ausgedrückt: Das Skalarprodukt aus Eingabevektor und Gewichtungsvektor minus dem Schwellenwert muss größer Null sein.
Das folgende Bild zeigt ein Beispiel eines Perceptrons mit drei Eingabewerten:
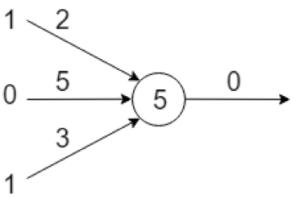
Die Berechnung des Ausgabewerts funktioniert wie oben beschrieben. Das Skalarprodukt aus Eingabe und Gewichtung ist ganz einfach 1 × 2 + 0 × 5 + 1 × 3 also 5. Damit der Ausgabewert des Perceptrons Eins wird, muss dieser Wert größer als der Schwellenwert sein. Da dieser hier fünf ist, ist der Ausgabewert Null.
Perceptrons kann man verbinden, d.h. man verwendet die Ausgabe eines Perceptrons als Eingabe eines anderen Perceptrons. Das Ergebnis ist ein neuronales Netz. Die Neuronen (hier Perceptrons) sind in Layern (Schichten) organisiert. Neuronen eines Layers sind mit allen anderen Neuronen des nächsten Layers verbunden, d.h. der Ausgabewert eines Neurons wird als ein Eingabewert von allen Neuronen des nächsten Layers verwendet. Entsprechend erhält ein Neuron so viele Eingabewerte wie es Neuronen im vorigen Layer gibt.
Wir unterscheiden hier drei Arten von Layern:
- Inputlayer: Die Neuronen in diesem Layer erhalten ihren Input als einzige nicht von anderen Neuronen, sondern von dem „Benutzer“ des NN. In diese werden die Eingaben in das NN kodiert, z.B. kann man mit N Neuronen ein einfaches Schwarz-Weiß Bild kodieren. Eine Eins als Input ist ein schwarzes Pixel, eine Null ein weißes.
- Outputlayer: Die Neuronen in diesem Layer geben ihren Output nicht an andere Neuronen weiter, sondern kodieren damit das Ergebnis des NN. Mit vier Neuronen im Outputlayer lässt sich zum Beispiel das Ergebnis einer Ziffernerkennung als Binärzahl kodieren.
- Hidden Layer: Alle Layer zwischen Input- und Outputlayer werden Hidden Layer genannt. Diese sind dazu da, das Ergebnis des NN zu den gelieferten Eingabedaten zu finden.
Mit diesem Wissen können wir uns nun vorstellen, wie ein NN anhand von Eingabedaten ein Ergebnis produziert:
- Das NN erhält seinen Input in die Neuronen des Inputlayers kodiert.
- Anhand der Gewichtungen und Schwellenwerte wird der Input für die Neuronen des nächsten Layers berechnet. Die Daten werden sozusagen von Layer zu Layer weitergeschoben. Dies wird so oft wiederholt, bis die Daten das Outputlayer erreicht haben.
- Der Benutzer des NN kann nun die Ausgabewerte der Neuronen im Outputlayer dekodieren und hat damit das Ergebnis vorliegen.
Im Folgenden ist ein solches NN schematisch dargestellt. Es kann immer nur jeweils ein Input- und Outputlayer, aber eine beliebige Anzahl von Hidden Layern geben.

Mit diesem einfachen Modell lassen sich schon viele Probleme lösen (auch Bilderkennung). Eine Frage ist aber noch offen: Woher kommen die Gewichtungen und Schwellenwerte?
Trainieren von neuronalen Netzwerken
Wir haben uns bis jetzt nur mit der Definition eines NN beschäftigt. Dort ist z.B. definiert wie viele Layer es gibt und wie viele Neuronen die einzelnen Layer haben. Auch die Kodierung der Daten in Input- und Outputlayer fällt darunter. Um das NN verwenden zu können, müssen die Gewichtungen und Schwellenwerte für jeden Neuron bestimmt werden, sodass das Netzwerk das Richtige tut. Dies geschieht durch das Trainieren des Netzwerks.
Beim Trainieren wird dem Netzwerk immer ein Inputdatensatz und zusätzlich das erwartete Ergebnis gegeben. Dies wird mit möglichst vielen Daten wiederholt. Durch einen speziellen Algorithmus – „Backpropagation“ genannt – belegt das Netzwerk die Gewichtungen und Schwellenwerte so, dass die Inputs des Netzwerks immer die gegebenen Outputs liefern. Die genaue Funktionsweise dieses Algorithmus ist relativ komplex, daher hier nur ein kurzer Überblick:
Zentrales Element ist eine sogenannte Loss-Funktion. Diese Funktion berechnet aus Ist- und Soll-Ausgabe des Netzwerks mit einer bestimmten Belegung einen Fehler. Ziel des Backpropagation Algorithmus ist nun, diesen Fehler zu minimieren, indem lokale Minima dieser Loss-Funktion berechnet werden.
Dadurch, dass die Funktionsweise allein von dem Trainingsdatensatz abhängt, ergeben sich einige sehr wichtige Anforderungen an die Trainingsdaten:
- Der Datensatz muss so groß wie möglich sein. Die Genauigkeit des Netzwerks wird deutlich besser je mehr Trainingsdaten man verwendet.
- Die Daten müssen so viele Eingabe-Ausgabe-Kombinationen abdecken wie möglich. In der Hinsicht funktioniert ein NN genauso wie ein natürliches Gehirn: Wenn es noch nie ein Katzenbild gesehen hat, kann es solche auch nicht klassifizieren.
- Die Daten dürfen keine anderen gemeinsamen Merkmale haben als das Merkmal, welches zu klassifizieren ist. Wenn beispielsweise Hundebilder immer eine hohe Helligkeit und Katzenbilder immer eine niedrige haben, kann es sein, dass das NN beim Klassifizieren die Helligkeit verwendet und das eigentliche Motiv ignoriert.
Die richtigen Trainingsdaten für ein NN zu finden ist nicht einfach. Es gibt zwar viele frei verfügbare Datensets im Internet, allerdings kann es sein, dass es für sehr spezifische Anwendungsfälle noch keine ausreichend großen Datensätze gibt. In diesem Fall müsste man sich selbst Datensets zusammenstellen, was je nach Anwendungsfall für Einzelpersonen oder Kleinunternehmen fast unmöglich sein kann. Für ein einfaches Problem, wie die bereits angesprochene Erkennung von handschriftlichen Ziffern, gibt es Datensätze, die bereits um die 50.000 Beispiele enthalten. Komplexere Probleme mit mehr möglichen Eingabe- und Ausgabeparametern (z. B. generische Bilderkennung) benötigen entsprechend ein Vielfaches an Beispielen.
Ergänzung: Sigmoid Neuronen
Das oben vorgestellte Konzept des Perceptrons ist zwar sehr einfach und gut zum Erklären von NN geeignet, in der Praxis allerdings nicht optimal. Es hat nämlich folgende Probleme:
- Kodierung von Eingabe- und Ausgabe ist schwierig, wenn nur binäre Belegungen möglich sind. Um den Zustand eines RGB-Pixels zu kodieren sind z.B. 24 Perceptrons nötig: Jeweils acht kodieren einen Farbwert als 8-Bit Binärzahl.
- Das Trainieren eines NN ist schwieriger, da durch die binären Werte kleine Änderungen an den Gewichtungen oder Schwellenwerte große Auswirkungen auf das Ergebnis des NN haben.
Diese Probleme lassen sich lösen, indem man, statt binärer Werte für die Neuronen, einen Wertebereich von Null bis Eins erlaubt. Das Berechnen des Outputs eines Neurons erfolgt weiter nach dem gleichen Schema: Die Gewichtungen werden mit allen Inputwerten multipliziert und dann addiert. Zusätzlich wird dieses Ergebnis allerdings noch in eine sogenannte Sigmoid-Funktion eingesetzt. Ohne diesen letzten Schritt könnten sonst Werte außerhalb des Wertebereichs von Null bis Eins entstehen. Die Sigmoid-Funktion überführt ihr Argument in diesen Wertebereich, indem große positive Zahlen asymptotisch gegen Eins laufen und große negative Zahlen analog gegen Null.
Mit diesem Modell lösen sich auch die beiden angeführten Probleme des Perceptron-Modells: Farbwerte von Pixeln lassen sich nun einfach in den Wertebereich Null bis Eins abbilden. Ein RGB-Pixel lässt sich nun mit drei statt 24 Neuronen kodieren.
Und auch das Trainieren ist einfacher: Eine Änderung in den Gewichtungen kann den Output eines Neurons nicht mehr ohne weiteres von Null auf Eins (oder anders herum) ändern. Stattdessen verringert sich der Output z.B. nur um 0,1.
Zusammenfassung
Wir haben nun alles zusammen, um zu verstehen, wie ein neuronales Netzwerk funktioniert:
- Ein NN besteht aus Neuronen, die in mehreren Layern organisiert sind.
- Alle Neuronen eines Layers geben ihren Output an alle Neuronen des nächsten Layers weiter.
- Jedes Neuron hat beliebig viele Inputs mit jeweils eigener Gewichtung, die sich alle einen Schwellenwert teilen. Auf dieser Basis wird der Output des Neurons berechnet.
- Die Belegung der Gewichtungen und Schwellenwerte eines NN erfolgt durch das Trainieren, indem dem Netzwerk eine große Menge von Eingaben mit erwarteten Ausgaben geliefert wird. Mit Hilfe eines Backpropagation-Algorithmus werden dann die Gewichtungen und Schwellenwerte so belegt, dass das Netzwerk eine möglich hohe Genauigkeit erreicht.
- Die Genauigkeit eines NN steht und fällt mit den Trainingsdaten. Je mehr und je besser die Trainingsdaten sind, desto höher fällt die Genauigkeit aus.
Eine Erkenntnis ist noch besonders wichtig: Ein fertig trainiertes NN ist eine Art Blackbox. Es ist praktisch unmöglich herauszufinden, wie genau das Netzwerk zu seinen Schlussfolgerungen kommt. Zwar hängt alles nur von den Gewichtungen und Schwellenwerten der Neuronen ab, aber die schiere Anzahl der Parameter macht es quasi unmöglich, die genauen Zusammenhänge zu durchschauen.
Buzzwords
Bei näherer Beschäftigung mit dem Thema stößt man unweigerlich auf viele verschiedene Begriffe, bei denen nicht immer sofort klar ist, was damit gemeint ist. Im Folgenden sind einige häufig vorkommende Begriffe kurz erklärt.
| Fully-Connected-Network (FCN) | Netzwerke, wie sie hier besprochen wurden, werden so genannt, da immer alle Neuronen eines Layers mit allen Neuronen des nächsten Layers verbunden sind. |
| Convolutional Neural Network (CNN) | Eine Weiterentwicklung von FCNs. CNNs berücksichtigen zusätzlich diese räumliche Struktur der Daten und es sind nicht immer alle Neuronen aufeinanderfolgender Layer miteinander verbunden. CNNs sind dadurch in vielerlei Hinsicht deutlich effizienter als FCNs. |
| Recurrent Neural Network | Normalerweise sind in NNs keine Rückkopplungen erlaubt, Neuronen geben ihren Output immer nur an das nächste Layer weiter. Bei dieser speziellen Form ist dies allerdings möglich, sodass das Netzwerk während der Arbeit weiter dazu lernen kann. |
| Machine Learning | Bezeichnet allgemein das Lösen von Problemen durch lernende Computerprogramme – meistens mit Hilfe neuronaler Netzwerke. |
| Deep Learning | Bezeichnet einen Pfad des Machine Learnings, der NNs verwendet, die sehr viele Layer haben. Da dies mit FCNs auf Grund von Designeinschränkungen nicht möglich ist, kommen dabei andere Typen wie CNNs zum Einsatz. |
| Supervised Learning | Eine Lehrmethode, bei der die Eingabe- und Ausgabewerte komplett vorgegeben werden. Ein Beispiel ist die hier vorgestellte Methode zum Trainieren von Neuronalen Netzwerken. Eignet sich für NNs, die Daten klassifizieren sollen. |
Frameworks und Ausblick
Mittlerweile gibt es mehrere Optionen, selbst die Möglichkeiten neuronaler Netzwerke zu nutzen, ohne sich mit den Details auskennen zu müssen. Frameworks wie Caffe (http://caffe.berkeleyvision.org/) oder Tensorflow (https://www.tensorflow.org/) machen es einfach, bereits fertig trainierte Modelle in eigene Anwendungen einzubinden. Darüber hinaus bieten sie natürlich auch Schnittstellen um eigene Modelle zu erstellen und zu trainieren. Berechnungen können wahlweise auch auf der Grafikkarte ausgeführt werden, so dass auch komplexere Aufgaben mit guter Performance erledigt werden können.
Projekte wie AlphaGo von Google DeepMind beweisen, dass neuronale Netzwerke großes Potential haben. AlphaGo ist ein Computerprogramm auf Basis neuronaler Netzwerke, dass das asiatische Brettspiel Go spielen kann. Bereits 2016 schlug AlphaGo einen der weltbesten Go-Spieler, was vorher lange Zeit als praktisch unmöglich galt. Go ist um ein Vielfaches komplexer als beispielsweise Schach und stellt sehr hohe Anforderungen an den Spieler. Nur ein Jahr später wurde eine Weiterentwicklung von AlphaGo „AlphaGo-Zero“ vorgestellt, die lediglich die Spielregeln kannte und auf kein anderes Vorwissen zurückgriff. Nach nur drei Tagen Training, in dem das Programm gegen sich selbst spielte, konnte es AlphaGo in 100 von 100 Spielen schlagen. Das Programm entwickelte dabei Strategien, von denen selbst Profispieler überrascht waren.
Die Möglichkeiten, die solche Verfahren bieten, sind schier endlos. Wir können gespannt sein, was uns in den nächsten Jahren auf dem Gebiet erwartet.
Titelbild: © Dmitrii Korolev – stock.adobe.com

Softwareentwicklung